Galería de Fractales
Geometría Fractal
La geometría fractal busca y estudia la regularidad en las relaciones entre un objeto y sus partes a diferentes escalas.
A fnales del siglo XIX surgieron conjuntos muy irregulares que poseían propiedades geométricas y analíticas sorprendentes. El primero de estos conjuntos fue el conjunto de Cantor (1890), y luego aparecieron otros tales como el triángulo de Sierpinski, curva de Koch, esponja de Menger, la curva de Peano, etc. A medida que se fueron creando las herramientas matemáticas necesarias para estudiarlos y comprenderlos, la teoría de Hausdorff y la teoría de Besicovitch, fue aumentando el interés por ellos. El origen de la geometría fractal o teoría geométrica de la medida está en el estudio de estos conjuntos irregulares y sus propiedades.
En 1977, B. Mandelbrot, en su obra “The fractal Geometry of Nature”, introdujo el término fractal designado a aquellos conjuntos de estructuras irregulares y complejas que no tenían ningún nombre concreto y desde entonces se conoce esta rama de las matemáticas como geometría fractal.
¿Qué es un Fractal?
Un fractal es un conjunto que tiene una o varias de las siguientes propiedades:
• Tiene detalles a todas las escalas.
• Es autosemejante.
• Tiene una definición algorítmica sencilla.
• Tiene dimensión topológica menor que su dimensión de Hausdorff.
En otras palabras, un fractal es un conjunto de estructuras irregulares y complejas descritas a través de algoritmos matemáticos y computacionales; los cuales reemplazan a los puntos, rectas, circunferencias y dem´as figuras provenientes de la matem´atica tradicional . Estos objetos tienen como caracter´ısticas fundamentales las propiedades de autosimilitud y la de convivir con extraños paisajes formados por dimensiones fraccionarias.
FRACTALES
Fractales de Newton
Fractal número 1

Función con la que se generó el fractal fue, $z^5-1$
Para este fractal se implementó el siguiente código:
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
imgx=800
imgy=800
image=Image.new("RGB",(imgx,imgy))
image.putpixel((100,100),(255,255,255))
image
xa=-1
xb=1
ya=-1
yb=1
maxit=202
h=1e-6
eps=1e-3
def f(z):
return z**5-1
for y in range (imgy):
zy=y*(yb-ya)/(imgy-1)+ya
for x in range (imgx):
zx=x*(xb-xa)/(imgx-1)+xa
z=complex(zx,zy)
for i in range (maxit):
dz=(f(z+complex(h,h))-f(z))/complex(h,h)
z0=z-f(z)/dz
if abs (z0-z)<eps:
break
z=z0
r=i*50
g=i*70
b=i*8
image.putpixel((x,y),(r,g,b))
image
Fractal número 2

La función con la cual se generó este fractal fue, $z^7-z^5-z^3-1$
Y el código que se implementó para generar el fractal fue:
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
imgx=800
imgy=800
image=Image.new("RGB",(imgx,imgy))
image.putpixel((100,100),(255,255,255))
image
xa=-1
xb=1
ya=-1
yb=1
maxit=202
h=1e-6
eps=1e-3
def f(z):
return z**7-z**5-z**3-1
for y in range (imgy):
zy=y*(yb-ya)/(imgy-1)+ya
for x in range (imgx):
zx=x*(xb-xa)/(imgx-1)+xa
z=complex(zx,zy)
for i in range (maxit):
dz=(f(z+complex(h,h))-f(z))/complex(h,h)
z0=z-f(z)/dz
if abs (z0-z)<eps:
break
z=z0
r=i*50
g=i*8
b=i*70
image.putpixel((x,y),(r,g,b))
Fractal número 3

La función con la cual se generó este fractal fue, $z^{15}-z^{13}-z^{11}-z^9-z^7-z^5-z^3-1$
Y el código que se implementó fue el siguiente:
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
imgx=800
imgy=800
image=Image.new("RGB",(imgx,imgy))
image.putpixel((100,100),(255,255,255))
image
xa=-1
xb=1
ya=-1
yb=1
maxit=202
h=1e-6
eps=1e-3
def f(z):
return z**15-z**13-z**11-z**9-z**7-z**5-z**3-1
for y in range (imgy):
zy=y*(yb-ya)/(imgy-1)+ya
for x in range (imgx):
zx=x*(xb-xa)/(imgx-1)+xa
z=complex(zx,zy)
for i in range (maxit):
dz=(f(z+complex(h,h))-f(z))/complex(h,h)
z0=z-f(z)/dz
if abs (z0-z)<eps:
break
z=z0
r=i*80
g=i*50
b=i*3
image.putpixel((x,y),(r,g,b)
Fractal número 4

La función con la cual se generó este fractal fue, $z^7-z^6+z^5-z^4+z^3-15$
Y el código que se implementó fue el siguiente:
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
imgx=800
imgy=800
image=Image.new("RGB",(imgx,imgy))
image.putpixel((100,100),(255,255,255))
image
xa=-1
xb=1
ya=-1
yb=1
maxit=202
h=1e-6
eps=1e-3
def f(z):
return z**7-z**6+z**5-z**4+z**3-15
for y in range (imgy):
zy=y*(yb-ya)/(imgy-1)+ya
for x in range (imgx):
zx=x*(xb-xa)/(imgx-1)+xa
z=complex(zx,zy)
for i in range (maxit):
dz=(f(z+complex(h,h))-f(z))/complex(h,h)
z0=z-f(z)/dz
if abs (z0-z)<eps:
break
z=z0
r=i*80
g=i*10
b=i*20
image.putpixel((x,y),(r,g,b))
Conjunto de Julia
Fractal número 1

La función con la cual se generó este fractal fue, $z^{10}+i$
Y el código que se implementó para este fractal fue:
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
xa=-1.2
xb=1.2
ya=-1.2
yb=1.2
maxit=30
def f(z):
return z**10+complex(0,1)
for y in range (imgy):
zy=y*(yb-ya)/(imgy-1)+ya
for x in range (imgx):
zx=x*(xb-xa)/(imgx-1)+xa
z=complex(zx,zy)
for i in range (maxit):
z0=f(z)
if abs(z)>1000:
break
z=z0
r=i*70
g=i*90
b=i*50
image.putpixel((x,y),(r,g,b))
Fractal número 2

La función con la cual se generó este fractal fue, $z^4+(0.3+0.5i)$
El código que se implementó para el fractal fue:
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
xa=-1.2
xb=1.2
ya=-1.2
yb=1.2
maxit=30
def f(z):
return z**4+complex(0.3,0.5)
for y in range (imgy):
zy=y*(yb-ya)/(imgy-1)+ya
for x in range (imgx):
zx=x*(xb-xa)/(imgx-1)+xa
z=complex(zx,zy)
for i in range (maxit):
z0=f(z)
if abs(z)>1000:
break
z=z0
r=i*50
g=i*8
b=i*8
image.putpixel((x,y),(r,g,b))
Fractal número 3

La función con la cual se generó este fractal fue, $z^5+i$
El código que se implementó para el fractal fue:
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
xa=-1.5
xb=1.5
ya=-1.5
yb=1.5
maxit=30
def f(z):
return z**5+complex(0,1)
for y in range (imgy):
zy=y*(yb-ya)/(imgy-1)+ya
for x in range (imgx):
zx=x*(xb-xa)/(imgx-1)+xa
z=complex(zx,zy)
for i in range (maxit):
z0=f(z)
if abs(z)>1000:
break
z=z0
r=i*8
g=i*55
b=i*50
image.putpixel((x,y),(r,g,b))
Fractal número 4
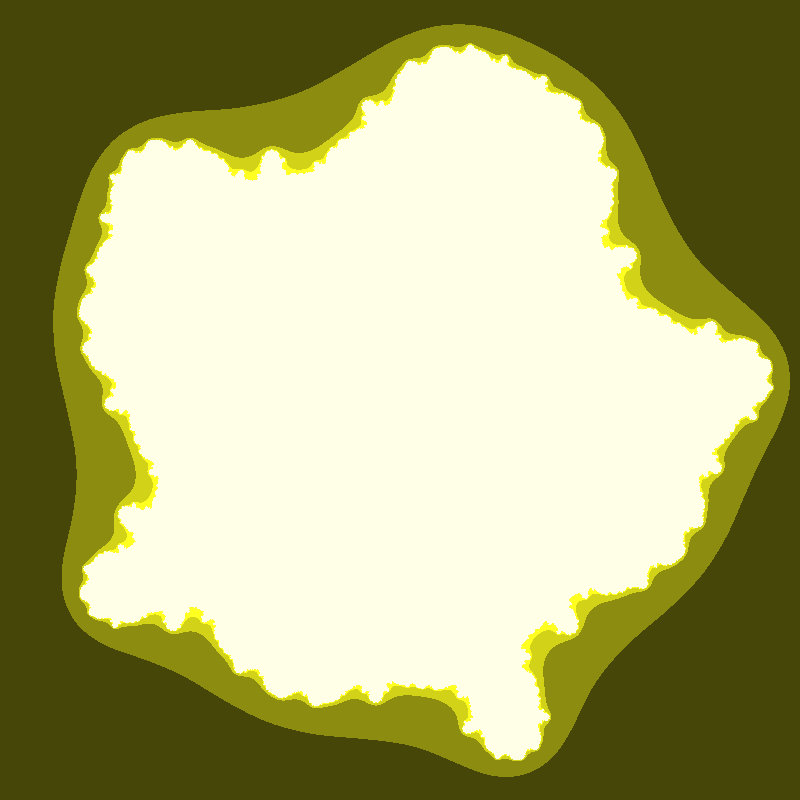
La función con la cual se generó este fractal fue, $z^9-z^4+0.5i$
El código que se implementó para este fractal fue:
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
xa=-1.2
xb=1.2
ya=-1.2
yb=1.2
maxit=30
def f(z):
return z**9-z**4+complex(0,0.5)
for y in range (imgy):
zy=y*(yb-ya)/(imgy-1)+ya
for x in range (imgx):
zx=x*(xb-xa)/(imgx-1)+xa
z=complex(zx,zy)
for i in range (maxit):
z0=f(z)
if abs(z)>1000:
break
z=z0
r=i*70
g=i*70
b=i*8
image.putpixel((x,y),(r,g,b))
Funciones Iteradas
Triángulo de Sierpinski
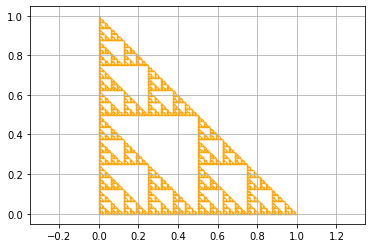
El código que se implementó para generar este fractal fue:
import numpy as np
import matplotlib.pyplot as plt
def transafin(M,t,x):
y=M@x+t
return y
transafin([[0.5,0],[0,0.5]],[0,0],Tri[1])
fig=plt.figure()
ax=plt.gca()
Tri=np.array([[0,0]])
for i in range(8):
tritrans=np.array([transafin([[0.5,0],[0,0.5]],[0,0],i) for i in Tri])
tritrans2=np.array([transafin([[0.5,0],[0,0.5]],[0,0.5],i) for i in Tri])
tritrans3=np.array([transafin([[0.5,0],[0,0.5]],[0.5,0],i) for i in Tri])
Tri=np.concatenate((tritrans,tritrans2,tritrans3))
plt.scatter(Tri.transpose()[0],Tri.transpose()[1],color='Orange',s=0.2)
ax.set_xticks(np.arange(-0.2,1.4,0.2))
ax.set_yticks(np.arange(-0.2,1.4,0.2))
plt.grid()
ax.axis("equal")
Helecho

El código que se implementó para generar este fractal fue:
import matplotlib.pyplot as plt
from random import randint
x = []
y = []
x.append(0)
y.append(0)
current = 0
for i in range(1, 50000):
z = randint(1, 100)
if z == 1:
x.append(0)
y.append(0.16*(y[current]))
if z>= 2 and z<= 86:
x.append(0.90*(x[current]) + 0.04*(y[current]))
y.append(-0.04*(x[current]) + 0.80*(y[current])+1.6)
if z>= 87 and z<= 93:
x.append(0.2*(x[current]) - 0.26*(y[current]))
y.append(0.23*(x[current]) + 0.22*(y[current])+1.6)
if z>= 94 and z<= 100:
x.append(-0.15*(x[current]) + 0.28*(y[current]))
y.append(0.20*(x[current]) + 0.10*(y[current])+0.44)
current = current + 1
plt.scatter(x, y, s = 0.2, edgecolor ='pink')
plt.axis("equal")
plt.show()
Curva de Von Koch
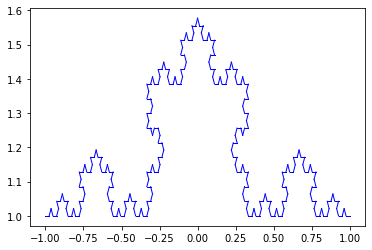
Para este fractal se implemento el siguiente código:
from math import sin, cos, pi, atan2
from pylab import *
def curvaVonKoch(xi, yi, xf, yf, n):
if n == 0:
plot([xi, xf], [yi, yf], lw=1.0, color='b')
elif n > 0:
x1 = xi + (xf - xi) / 3.0
y1 = yi + (yf - yi) / 3.0
x3 = xf - (xf - xi) / 3.0
y3 = yf - (yf - yi) / 3.0
radio = hypot(x3 - x1, y3 - y1)
alpha = atan2((y3 - y1), (x3 - x1))
alpha += pi / 3.0
x2 = x1 + radio * cos(alpha)
y2 = y1 + radio * sin(alpha)
curvaVonKoch(xi, yi, x1, y1, n - 1)
curvaVonKoch(x1, y1, x2, y2, n - 1)
curvaVonKoch(x2, y2, x3, y3, n - 1)
curvaVonKoch(x3, y3, xf, yf, n - 1)
return
Copo de Von Koch

El código que se implementó para este fractal fue:
from math import sin, cos, pi, atan2
from pylab import *
def copoVonKoch(lado, n):
x_vertice1 = 0
y_vertice1 = 0
x_vertice2 = lado * cos(2 * pi / 3)
y_vertice2 = lado * sin(2 * pi / 3)
x_vertice3 = lado * cos(pi / 3)
y_vertice3 = lado * sin(pi / 3)
(x_vertice1, y_vertice1, x_vertice2, y_vertice2, n)
curvaVonKoch(x_vertice2, y_vertice2, x_vertice3, y_vertice3, n)
curvaVonKoch(x_vertice3, y_vertice3, x_vertice1, y_vertice1, n)
return
Fractal 3D

Paa generar este fracta el 3D se implementó el siguiente código:
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.view_init(azim=150,elev=60)
ax.dist = 3.5
ax.set_facecolor([0.5,0.0,0.0])
n = 9
dx = 0.0
dy = 0.0
L = 2.0
M = 200
def f(Z):
return np.e**(-np.abs(Z))
x = np.linspace(-L+dx,L+dx,M)
y = np.linspace(-L+dy,L+dy,M)
X,Y = np.meshgrid(x,y)
cX = -0.7454294
cY = 0
C = cX + 1j*cY
W = np.zeros((M,M))
Z = X + 1j*Y
for k in range(1,n+1):
ZZ = Z**2 + C
Z = ZZ
W = f(Z)
ax.set_xlim(dx-L,dx+L)
ax.set_zlim(dy-L,dy+L)
ax.set_zlim(-2*L,2*L)
ax.axis("off")
ax.plot_surface(X, Y, -W, rstride=1, cstride=1, cmap="Oranges")
plt.show()